Kepler le somnambule
Découvreur malgré soi
Il n’existe ni théorie ni méthode de la découverte scientifique. Ceci parce que découvrir consiste par définition trouver du nouveau, donc précisément ce que l’on n’attendait pas. L’astronome allemand Johannes Kepler (1571 – 1630) illustre ce paradoxe du découvreur malgré soi.
Le 1er janvier 1600, Kepler quitte sa ville natale de Gratz où il vit, pour se rendre à Benatek, non loin de Prague, auprès de l’astronome danois Tycho Brahé (1546 – 1601). Cette rencontre entre deux géants de l’astronomie orientera le cours de l’histoire des sciences. Kepler n’aurait rien été sans Tycho Brahé, le travail de Tycho Brahé serait resté vain sans le génie de Kepler pour en extraire la substantifique moelle.
Nul ne connaît l’avenir et bien des scientifiques ont été conduits par leurs travaux vers des horizons qu’ils ne recherchaient pas. Aussi se réveillèrent-ils comme des somnambules, bien loin de leur objectif. À lire l’ouvrage désormais classique d’Arthur Koestler Les Somnambules, qui taille une large place à Kepler, on a le sentiment que l’auteur voit dans la figure attachante de Kepler le plus somnambule des somnambules. Le savant allemand semble en effet s’ingénier pendant de longues années à ne pas trouver les fameuses lois qui immortaliseront son nom. Curieuse trajectoire.
Tycho Brahé ne conquit pas la renommée de son illustre disciple. C’est justice, car il n’eut rien d’un inventeur. Il appartient à cette lignée de scientifiques sans génie qui servent la science en s’attachant à un travail de mesure long et difficile mais nécessaire. Tycho Brahé, sous l’hivernal ciel danois, passera trente années à scruter les astres et à mesurer leurs positions. À son époque, les meilleures mesures astrales datent de l’Antiquité. Pour les améliorer, Tycho Brahé conçoit lui-même son appareillage. Il a pris connaissance de la théorie héliocentrique de Copernic et comprend que le renouvellement de l’astronomie qui se prépare aura besoin de mesures fines. Le talent de Tycho consiste à concevoir des appareils qui améliorent de beaucoup la précision des mesures. La science appelle ces deux sortes de chevaliers servants : les Tycho, sérieux, ingénieux, infiniment patients et les Kepler, géniaux, inspirés, parfois brouillons. Le hasard d’une époque les réunit.
La perfection dans l’ineptie
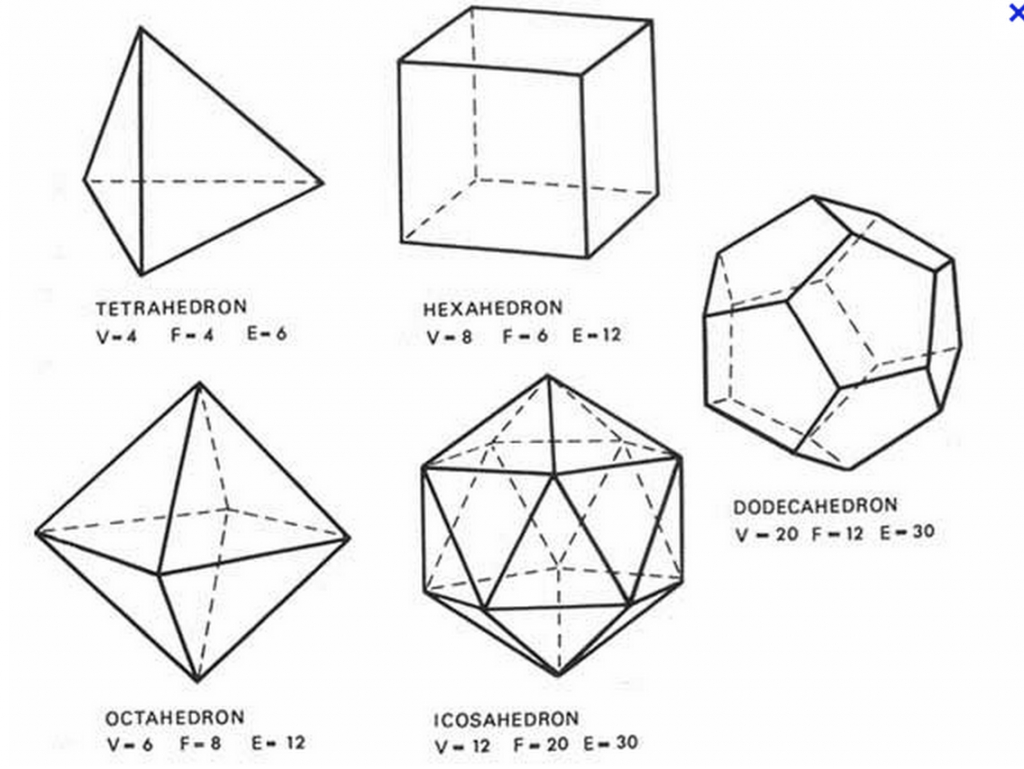
Avant sa rencontre avec Tycho, Kepler a publié Le Mystère cosmographique en 1597, ouvrage dans lequel il traque les desseins de l’Architecte de l’univers. Thèse de Kepler : le Très-Haut n’a pu concevoir qu’un monde harmonieux, à l’image de sa propre perfection. Il existe six planètes dont les orbites sont nécessairement circulaires. Mais pourquoi Dieu s’est-il arrêté au nombre six ? Kepler sait par ailleurs qu’il existe cinq polyèdres réguliers, c’est-à-dire cinq polyèdres convexes composés de faces toutes identiques : le tétraèdre (quatre faces triangulaires), le cube (six faces carrées), l’octaèdre (huit faces triangulaires), le dodécaèdre (douze faces pentagonales) et l’icosaèdre (vingt faces triangulaires) (cf. figure 1).
Figure 1
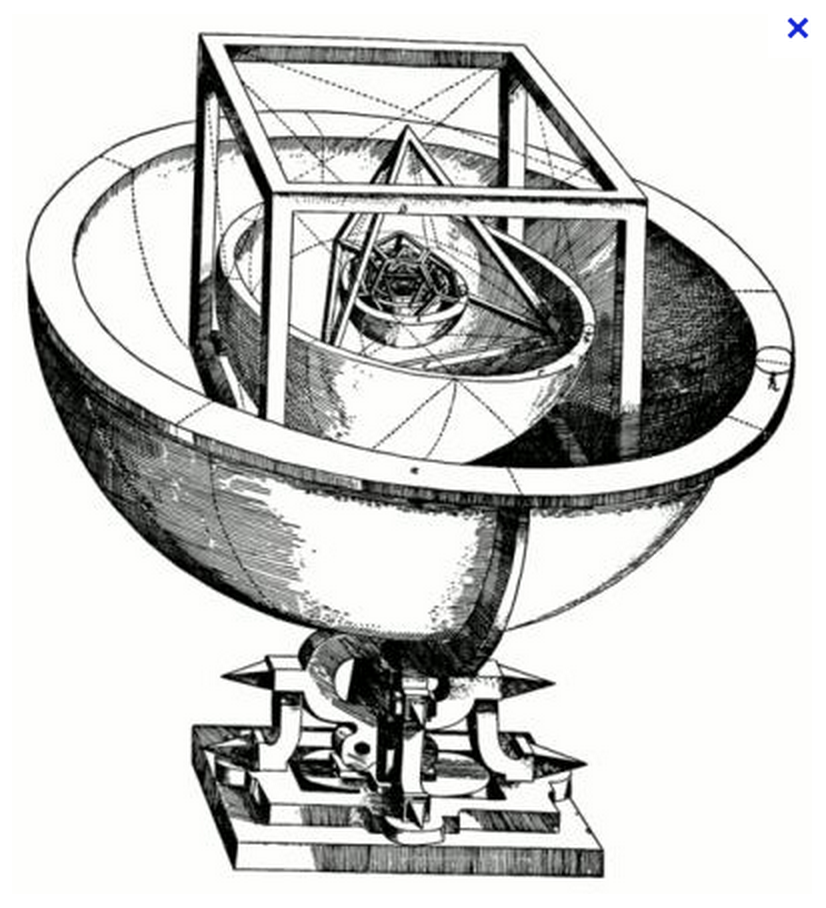
Il est clair – pour Kepler au moins – que ces polyèdres réguliers forment l’ensemble des volumes parfaits. Le savant rapproche cette perfection de celle – présumée ! – de l’univers et le nombre cinq des polyèdres réguliers du nombre six des planètes. Kepler croit avoir percé le plan divin : on déduit l’orbite d’une planète de celle de la planète supérieure à l’aide d’un polyèdre régulier. La planète supérieure évolue sur une sphère qui passe par les sommets du polyèdre et la planète inférieure sur une sphère tangente aux faces (cf. figure 2).
Figure 2
On passe ainsi de l’orbe de Saturne à celle de Jupiter par un cube. Le cube se trouve à l’extérieur car il est le plus élevé en dignité : les angles de ses faces sont les mêmes que ceux de ses plans : comme l’animal et l’homme, il comporte six côtés, haut, bas, arrière, avant, droite, gauche. On passe de l’orbe de Jupiter à celle de Mars par un tétraèdre car, dit Kepler, les trigones du tétraèdre correspondent au caractère bénéfique de Jupiter. On apprend qu’il faut distinguer, parmi les cinq polyèdres réguliers, le cube, le tétraèdre et le dodécaèdre d’une part, l’icosaèdre et l’octaèdre de l’autre. Les premiers sont dits « primaires », parce qu’il sont construits à l’aide de polygones différents (carré, triangle et pentagone) et comportent un nombre minimum de faces. En revanche, les deux derniers sont secondaires et de la même famille que le tétraèdre puisque composés comme lui de triangles équilatéraux. Il est « naturel » que l’orbe de la Terre soit placée entre les uns et les autres – séparant ainsi deux régions du monde – et qu’il y ait au-dessus d’elle trois astres (Mars, Jupiter et Saturne) et trois en dessous (Venus, Mercure et le Soleil) puisqu’elle est le séjour de l’homme, « but du monde et de la création ».
On passe donc de l’orbite de Mars à celle de la Terre par un dodécaèdre, seul polyèdre primaire restant, de l’orbe de la Terre à celle de Vénus par l’icosaèdre et de l’orbe de Vénus à celle de Mercure par un octaèdre.
Pour séduisante qu’elle soit à un esprit de la Renaissance, cette architecture impeccable coïncide cependant mal avec les mesures – même imprécises – dont dispose Kepler. On est obligé de supposer une certaine épaisseur aux sphères séparant les polyèdres, ce qui ôte de la perfection à la construction divine. Pourquoi Dieu n’a-t-il pas choisi une perfection parfaite ?
Subtilité ou malveillance de Dieu
Comme le dira plus tard Einstein : « Dieu est subtil mais il n’est pas malveillant. » Devant les difficultés, Kepler se convaincra que sa subtilité n’a pas encore égalée celle du Très-Haut et il reprendra sa quête. Surtout, il attend que Tycho lui livre ses mesures, ne doutant pas qu’elles lui permettront de percer rapidement le secret de l’univers. La rencontre de ces deux hommes que leurs tempéraments opposent – l’impitoyable bon vivant Tycho sourit de l’intellectuel souffreteux Kepler – constitue un moment pittoresque de l’histoire des sciences. Pendant plus d’un an, Tycho garde pour lui ses livres de mesures, lâchant au malheureux Kepler une donnée de temps à autre, jouant au chat et à la souris avec le jeune savant devenu souris de laboratoire.
Tycho a sans doute reconnu les exceptionnelles qualités de mathématicien de Kepler. Il compte les utiliser mais il les redoute. Il ne s’agit pas seulement d’une jalousie de savant et de la crainte de voir Kepler tirer à soi toute la gloire ; ce qui sera finalement le cas. Un différend scientifique de fond oppose Kepler à Tycho Brahé. Kepler est un héliocentriste convaincu, il connaît les idées de Copernic et ne doute pas que les planètes tournent autour du Soleil. Son ingénieuse construction à partir des polyèdres est, on l’a vu, de conception héliocentrique.
Le monde selon Tycho Brahé
Tycho Brahé quant à lui sait bien que le modèle héliocentrique permet de comprendre certains phénomènes curieux tel le mouvement rétrograde des planètes. Il a lui-même fait des observations qui disqualifient définitivement la vision aristotélicienne de l’univers. En 1572, il a observé l’apparition puis la disparition d’une étoile, ce qui prouve que le monde supralunaire n’est pas immuable. Tycho sait que les comètes qu’il a observées traversent les orbites planétaires, ce qui montre que les orbes solides des planètes n’existent pas.
Cependant il est sensible aux objections que la physique de l’époque – la physique aristotélicienne – oppose au mouvement de la Terre. Ces objections se ramènent à un argument frappant pour le sens commun : si la Terre se meut, comment se fait-il que nous Terriens de modeste facture ne nous en apercevions pas, qu’il n’y ait sur Terre aucune conséquence sensible de ce mouvement ? Il est impossible de réfuter cette objection compte tenu des connaissances scientifiques de l’époque. Tycho, qui patiemment a relevé les meilleures mesures astronomiques jamais faites, a par ailleurs cherché en vain à mettre en évidence le mouvement de parallaxe des étoiles proches, mouvement qui devrait résulter de la théorie copernicienne.
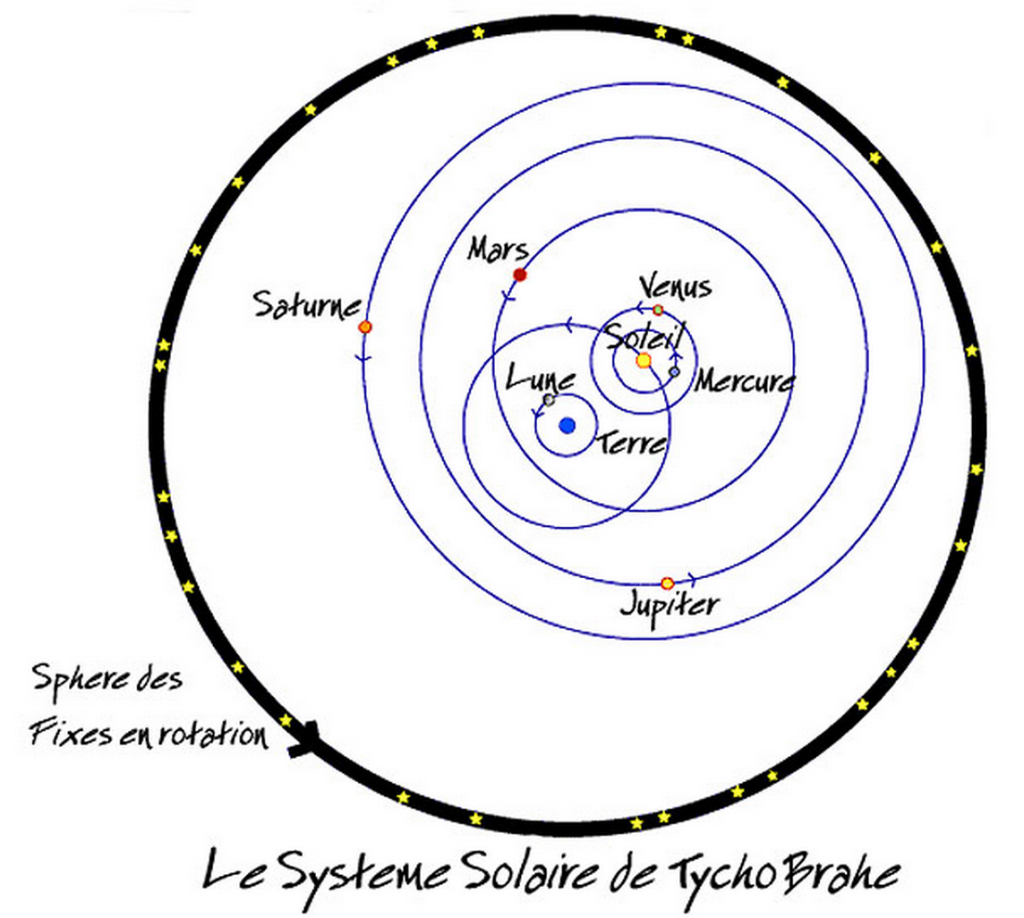
Aussi Tycho Brahé tente-t-il de concilier les avantages des deux modèles par un modèle intermédiaire. Soit, la Terre est immobile et le Soleil tourne bien autour d’elle. Mais les autres planètes, elles, tournent autour du Soleil (cf. figure 3).
Figure 3
Tycho propose entre les systèmes de Ptolémée et de Copernic un compromis qui évite les objections opposées à l’un et à l’autre. Il tient beaucoup à son idée et craint que Kepler utilise ses propres mesures pour la réfuter.
Le somnambule en marche
Tycho Brahé meurt le 24 octobre 1601 dans des circonstances rocambolesques sur lesquelles le romancier Milan Kundera a écrit quelques pages non moins rocambolesques. Mais peu importent les circonstances en l’occurrence, il reste que Kepler n’en a cure et qu’il subtilise les livres de mesure avant que le cadavre ne soit refroidi, au nez et à la barbe des héritiers furieux. Alors commence pour lui de longues années d’un travail de titan. Kepler se bat avec les mesures de Tycho, échafaudant des hypothèses, se trompant dans ses calculs, abandonnant une idée pour un écart de huit minutes avec les mesures. Une de ses idées fructueuses consiste à considérer le mouvement des planètes par rapport au Soleil plutôt que par rapport au centre de l’orbite terrestre. Il raconte son cheminement dans un livre baroque publié en 1609 L’Astronomie Nouvelle. Dans ces pages, il retrace point par point toutes les étapes, les impasses, les erreurs de calcul qui l’ont conduit finalement au succès. Deux lois, dites lois de Kepler, n’apparaissent qu’à la fin du livre, noyées dans le fouillis général (la troisième loi ne paraîtra que plus tard). L’étape décisive et sans doute la plus difficile fut pour Kepler l’abandon des orbites circulaires. Il ne dissimule pas la difficulté qu’il eut à établir ces lois et l’étrangeté des plans divins ainsi découverts qui laissent peu de place à l’harmonie et la perfection.
Voici les trois lois qui immortaliseront le nom de Kepler. Première loi : les planètes décrivent des ellipses dont le Soleil occupe un des foyers. Deuxième loi : leurs rayons balaient des aires égales en des temps égaux (contrairement aux femmes de ménage). Troisième loi : le carré de leur période de révolution est proportionnel au cube du grand axe de l’ellipse.
Le succès est incontestable. Mais curieusement, le livre de Kepler – tout comme cet article – n’assura sur le moment aucune gloire à son auteur et ne jouera nul rôle lors des démêlés de Galilée avec l’Église. Galilée, esprit jaloux dont la contribution à l’astronomie théorique est quasi nulle, n’avait pas lu L’Astronomie Nouvelle. Il n’en tira donc pas argument et ne cite pas le livre dans son Dialogue sur les deux principaux systèmes du monde de 1632.
Ce faible renom explique en partie que Kepler ait échappé aux ennuis dont souffrit Galilée. Prudent sans doute, Kepler ne s’aventura pas sur le terrain théologique et se garda bien de narguer les adversaires de l’héliocentrisme comme le fit Galilée. La hargne du savant italien vers 1615 peut expliquer la réaction de l’Église à partir de 1616. En 1609, le Saint-Office ne s’intéresse pas aux idées héliocentriques de Kepler.
Kepler poursuivra sa vie plus ou moins misérable d’astronome plus ou moins officiel, passant de ville en ville au gré des guerres de religion, se débattant contre la pauvreté et l’Inquisition pour arracher au bûcher sa mère accusée de sorcellerie.
Cette relative indifférence vis-à-vis de ce qui nous paraît si essentiel dans l’œuvre de Kepler a au moins trois raisons.
Tout d’abord, comme tous les astronomes de son temps, Kepler est aussi astrologue. L’astrologie seule intéresse les grands qui le payent. Kepler consacre donc une grande part de son activité à l’astrologie, qu’il tente de rationaliser en imaginant les mécanismes d’influence des astres sur notre destin. L’œuvre de Kepler est essentiellement astrologique et peu sont capables à l’époque de discerner dans ce fatras le joyau que constituent les trois lois.
Ensuite ces lois sont descriptives plutôt qu’explicatives. C’est dire qu’elles n’ont pas force de preuve dans l’assaut que mène Galilée contre la vision géocentrique du monde. Kepler décrit le mouvement des planètes par rapport au Soleil. Soit. Mais cela ne prouve pas que le Soleil soit le centre du monde. Galilée s’est embarqué sans le savoir dans une querelle sans espoir car il n’existe pas, on le sait aujourd’hui, d’immobilité absolue, donc de centre de l’univers.
Enfin Kepler ne propose pas d’explication commune à ses trois lois. Dans certains de ses écrits, il est proche de l’intuition de la fore gravitationnelle. Mais au dernier moment, le Moyen Âge ou le sens commun le tire par les pieds et l’empêche d’envisager l’hypothèse, peu vraisemblable mais féconde ô combien, de l’attraction gravitationnelle. Kepler est mort trop tôt pour connaître les travaux de Galilée sur la chute des corps, qui auraient pu l’aider. C’est donc à Newton, qui n’ignorait rien des travaux de Kepler et de Galilée, que revint la gloire d’unifier l’astronomie et la mécanique et un corpus commun. Cela se passait en 1686.
On peut bien sûr regretter que Kepler et Galilée n’aient pas uni leurs efforts et porté plus loin leur assaut pour investir la forteresse de la physique nouvelle. Ils ne se sont jamais rencontrés ; l’orgueilleux Galilée, qui laissait sans réponse les lettres de Kepler, en porte la responsabilité.
Comme on ne modifie pas souvent le passé, Galilée et Kepler n’étaient pas nés pour s’entendre mais ensemble ils ouvrirent la voie à Newton, somnambule champêtre qu’une pomme éveilla.